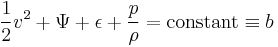Bernoulli's principle

In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy.[1][2] Bernoulli's principle is named after the Dutch-Swiss mathematician Daniel Bernoulli who published his principle in his book Hydrodynamica in 1738.[3]
Bernoulli's principle can be applied to various types of fluid flow, resulting in what is loosely denoted as Bernoulli's equation. In fact, there are different forms of the Bernoulli equation for different types of flow. The simple form of Bernoulli's principle is valid for incompressible flows (e.g. most liquid flows) and also for compressible flows (e.g. gases) moving at low Mach numbers. More advanced forms may in some cases be applied to compressible flows at higher Mach numbers (see the derivations of the Bernoulli equation).
Bernoulli's principle can be derived from the principle of conservation of energy. This states that in a steady flow the sum of all forms of mechanical energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy and potential energy remain constant. If the fluid is flowing out of a reservoir the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit mass (the sum of pressure and gravitational potential ρ g h) is the same everywhere.[4]
Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.
Contents |
Incompressible flow equation
In most flows of liquids, and of gases at low Mach number, the mass density of a fluid parcel can be considered to be constant, regardless of pressure variations in the flow. For this reason the fluid in such flows can be considered to be incompressible and these flows can be described as incompressible flow. Bernoulli performed his experiments on liquids and his equation in its original form is valid only for incompressible flow. A common form of Bernoulli's equation, valid at any arbitrary point along a streamline where gravity is constant, is:
-
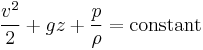
(
where:
 is the fluid flow speed at a point on a streamline,
is the fluid flow speed at a point on a streamline, is the acceleration due to gravity,
is the acceleration due to gravity, is the elevation of the point above a reference plane, with the positive z-direction pointing upward — so in the direction opposite to the gravitational acceleration,
is the elevation of the point above a reference plane, with the positive z-direction pointing upward — so in the direction opposite to the gravitational acceleration, is the pressure at the point, and
is the pressure at the point, and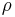 is the density of the fluid at all points in the fluid.
is the density of the fluid at all points in the fluid.
For conservative force fields, Bernoulli's equation can be generalized as:[5]
where Ψ is the force potential at the point considered on the streamline. E.g. for the Earth's gravity Ψ = gz.
The following two assumptions must be met for this Bernoulli equation to apply:[5]
- the fluid must be incompressible — even though pressure varies, the density must remain constant along a streamline;
- friction by viscous forces has to be negligible.
By multiplying with the fluid density 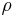 , equation (A) can be rewritten as:
, equation (A) can be rewritten as:
or:
where:
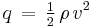 is dynamic pressure,
is dynamic pressure,
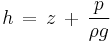 is the piezometric head or hydraulic head (the sum of the elevation z and the pressure head)[6][7] and
is the piezometric head or hydraulic head (the sum of the elevation z and the pressure head)[6][7] and
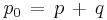 is the total pressure (the sum of the static pressure p and dynamic pressure q).[8]
is the total pressure (the sum of the static pressure p and dynamic pressure q).[8]
The constant in the Bernoulli equation can be normalised. A common approach is in terms of total head or energy head H:
The above equations suggest there is a flow speed at which pressure is zero, and at even higher speeds the pressure is negative. Most often, gases and liquids are not capable of negative absolute pressure, or even zero pressure, so clearly Bernoulli's equation ceases to be valid before zero pressure is reached. In liquids—when the pressure becomes too low -- cavitation occurs. The above equations use a linear relationship between flow speed squared and pressure. At higher flow speeds in gases, or for sound waves in liquid, the changes in mass density become significant so that the assumption of constant density is invalid.
Simplified form
In many applications of Bernoulli's equation, the change in the ρ g z term along the streamline is so small compared with the other terms it can be ignored. For example, in the case of aircraft in flight, the change in height z along a streamline is so small the ρ g z term can be omitted. This allows the above equation to be presented in the following simplified form:
where p0 is called total pressure, and q is dynamic pressure[9]. Many authors refer to the pressure p as static pressure to distinguish it from total pressure p0 and dynamic pressure q. In Aerodynamics, L.J. Clancy writes: "To distinguish it from the total and dynamic pressures, the actual pressure of the fluid, which is associated not with its motion but with its state, is often referred to as the static pressure, but where the term pressure alone is used it refers to this static pressure."[10]
The simplified form of Bernoulli's equation can be summarized in the following memorable word equation:
- static pressure + dynamic pressure = total pressure[10]
Every point in a steadily flowing fluid, regardless of the fluid speed at that point, has its own unique static pressure p and dynamic pressure q. Their sum p + q is defined to be the total pressure p0. The significance of Bernoulli's principle can now be summarized as total pressure is constant along a streamline.
If the fluid flow is irrotational, the total pressure on every streamline is the same and Bernoulli's principle can be summarized as total pressure is constant everywhere in the fluid flow.[11] It is reasonable to assume that irrotational flow exists in any situation where a large body of fluid is flowing past a solid body. Examples are aircraft in flight, and ships moving in open bodies of water. However, it is important to remember that Bernoulli's principle does not apply in the boundary layer or in fluid flow through long pipes.
If the fluid flow at some point along a stream line is brought to rest, this point is called a stagnation point, and at this point the total pressure is equal to the stagnation pressure.
Applicability of incompressible flow equation to flow of gases
Bernoulli's equation is sometimes valid for the flow of gases: provided that there is no transfer of kinetic or potential energy from the gas flow to the compression or expansion of the gas. If both the gas pressure and volume change simultaneously, then work will be done on or by the gas. In this case, Bernoulli's equation—in its incompressible flow form—can not be assumed to be valid. However if the gas process is entirely isobaric, or isochoric, then no work is done on or by the gas, (so the simple energy balance is not upset). According to the gas law, an isobaric or isochoric process is ordinarily the only way to ensure constant density in a gas. Also the gas density will be proportional to the ratio of pressure and absolute temperature, however this ratio will vary upon compression or expansion, no matter what non-zero quantity of heat is added or removed. The only exception is if the net heat transfer is zero, as in a complete thermodynamic cycle, or in an individual isentropic (frictionless adiabatic) process, and even then this reversible process must be reversed, to restore the gas to the original pressure and specific volume, and thus density. Only then is the original, unmodified Bernoulli equation applicable. In this case the equation can be used if the flow speed of the gas is sufficiently below the speed of sound, such that the variation in density of the gas (due to this effect) along each streamline can be ignored. Adiabatic flow at less than Mach 0.3 is generally considered to be slow enough.
Unsteady potential flow
The Bernoulli equation for unsteady potential flow is used in the theory of ocean surface waves and acoustics.
For an irrotational flow, the flow velocity can be described as the gradient ∇φ of a velocity potential φ. In that case, and for a constant density ρ, the momentum equations of the Euler equations can be integrated to:[12]
which is a Bernoulli equation valid also for unsteady—or time dependent—flows. Here ∂φ/∂t denotes the partial derivative of the velocity potential φ with respect to time t, and v = |∇φ| is the flow speed. The function f(t) depends only on time and not on position in the fluid. As a result, the Bernoulli equation at some moment t does not only apply along a certain streamline, but in the whole fluid domain. This is also true for the special case of a steady irrotational flow, in which case f is a constant.[12]
Further f(t) can be made equal to zero by incorporating it into the velocity potential using the transformation
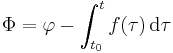 resulting in
resulting in 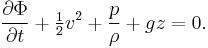
Note that the relation of the potential to the flow velocity is unaffected by this transformation: ∇Φ = ∇φ.
The Bernoulli equation for unsteady potential flow also appears to play a central role in Luke's variational principle, a variational description of free-surface flows using the Lagrangian (not to be confused with Lagrangian coordinates).
Compressible flow equation
Bernoulli developed his principle from his observations on liquids, and his equation is applicable only to incompressible fluids, and compressible fluids at very low speeds (perhaps up to 1/3 of the sound speed in the fluid). It is possible to use the fundamental principles of physics to develop similar equations applicable to compressible fluids. There are numerous equations, each tailored for a particular application, but all are analogous to Bernoulli's equation and all rely on nothing more than the fundamental principles of physics such as Newton's laws of motion or the first law of thermodynamics.
Compressible flow in fluid dynamics
For a compressible fluid, with a barotropic equation of state, and under the action of conservative forces,
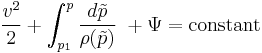 [13] (constant along a streamline)
[13] (constant along a streamline)
where:
- p is the pressure
- ρ is the density
- v is the flow speed
- Ψ is the potential associated with the conservative force field, often the gravitational potential
In engineering situations, elevations are generally small compared to the size of the Earth, and the time scales of fluid flow are small enough to consider the equation of state as adiabatic. In this case, the above equation becomes
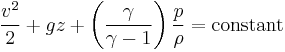 [14] (constant along a streamline)
[14] (constant along a streamline)
where, in addition to the terms listed above:
- γ is the ratio of the specific heats of the fluid
- g is the acceleration due to gravity
- z is the elevation of the point above a reference plane
In many applications of compressible flow, changes in elevation are negligible compared to the other terms, so the term gz can be omitted. A very useful form of the equation is then:
where:
- p0 is the total pressure
- ρ0 is the total density
Compressible flow in thermodynamics
Another useful form of the equation, suitable for use in thermodynamics, is:
Here w is the enthalpy per unit mass, which is also often written as h (not to be confused with "head" or "height").
Note that 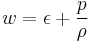 where ε is the thermodynamic energy per unit mass, also known as the specific internal energy or "sie."
where ε is the thermodynamic energy per unit mass, also known as the specific internal energy or "sie."
The constant on the right hand side is often called the Bernoulli constant and denoted b. For steady inviscid adiabatic flow with no additional sources or sinks of energy, b is constant along any given streamline. More generally, when b may vary along streamlines, it still proves a useful parameter, related to the "head" of the fluid (see below).
When the change in Ψ can be ignored, a very useful form of this equation is:
where w0 is total enthalpy. For a calorically perfect gas such as an ideal gas, the enthalpy is directly proportional to the temperature, and this leads to the concept of the total (or stagnation) temperature.
When shock waves are present, in a reference frame in which the shock is stationary and the flow is steady, many of the parameters in the Bernoulli equation suffer abrupt changes in passing through the shock. The Bernoulli parameter itself, however, remains unaffected. An exception to this rule is radiative shocks, which violate the assumptions leading to the Bernoulli equation, namely the lack of additional sinks or sources of energy.
Derivations of Bernoulli equation
-
Bernoulli equation for incompressible fluids The Bernoulli equation for incompressible fluids can be derived by integrating the Euler equations, or applying the law of conservation of energy in two sections along a streamline, ignoring viscosity, compressibility, and thermal effects. The simplest derivation is to first ignore gravity and consider constrictions and expansions in pipes that are otherwise straight, as seen in Venturi effect. Let the x axis be directed down the axis of the pipe.
The equation of motion for a parcel of fluid, having a length dx, mass density ρ, mass m = ρ A dx and flow velocity v = dx / dt, moving along the axis of the horizontal pipe, with cross-sectional area A is
In steady flow, v = v(x) so
With density ρ constant, the equation of motion can be written as
or
where C is a constant, sometimes referred to as the Bernoulli constant. It is not a universal constant, but rather a constant of a particular fluid system. The deduction is: where the speed is large, pressure is low and vice versa.
In the above derivation, no external work-energy principle is invoked. Rather, Bernoulli's principle was inherently derived by a simple manipulation of the momentum equation.
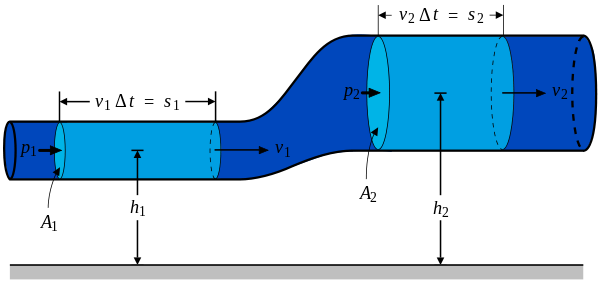 A streamtube of fluid moving to the right. Indicated are pressure, elevation, flow speed, distance (s), and cross-sectional area. Note that in this figure elevation is denoted as h, contrary to the text where it is given by z.
A streamtube of fluid moving to the right. Indicated are pressure, elevation, flow speed, distance (s), and cross-sectional area. Note that in this figure elevation is denoted as h, contrary to the text where it is given by z.Another way to derive Bernoulli's principle for an incompressible flow is by applying conservation of energy.[16] In the form of the work-energy theorem, stating that[17]
- the change in the kinetic energy Ekin of the system equals the net work W done on the system;
Therefore,
- the work done by the forces in the fluid = increase in kinetic energy.
The system consists of the volume of fluid, initially between the cross-sections A1 and A2. In the time interval Δt fluid elements initially at the inflow cross-section A1 move over a distance s1 = v1 Δt, while at the outflow cross-section the fluid moves away from cross-section A2 over a distance s2 = v2 Δt. The displaced fluid volumes at the inflow and outflow are respectively A1 s1 and A2 s2. The associated displaced fluid masses are—when ρ is the fluid's mass density -- equal to density times volume, so ρ A1 s1 and ρ A2 s2. By mass conservation, these two masses displaced in the time interval Δt have to be equal, and this displaced mass is denoted by Δm:
The work done by the forces consists of two parts:
- The work done by the pressure acting on the area's A1 and A2
- The work done by gravity: the gravitational potential energy in the volume A1 s1 is lost, and at the outflow in the volume A2 s2 is gained. So, the change in gravitational potential energy ΔEpot,gravity in the time interval Δt is
- Now, the work by the force of gravity is opposite to the change in potential energy, Wgravity = −ΔEpot,gravity: while the force of gravity is in the negative z-direction, the work--gravity force times change in elevation--will be negative for a positive elevation change Δz = z2 − z1, while the corresponding potential energy change is positive.[18] So:
And the total work done in this time interval
 is
isThe increase in kinetic energy is
Putting these together, the work-kinetic energy theorem W = ΔEkin gives:[16]
or
After dividing by the mass Δm = ρ A1 v1 Δt = ρ A2 v2 Δt the result is:[16]
or, as stated in the first paragraph:
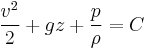 (Eqn. 1)
(Eqn. 1)
Further division by g produces the following equation. Note that each term can be described in the length dimension (such as meters). This is the head equation derived from Bernoulli's principle:
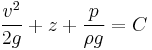 (Eqn. 2a)
(Eqn. 2a)
The middle term, z, represents the potential energy of the fluid due to its elevation with respect to a reference plane. Now, z is called the elevation head and given the designation zelevation.
A free falling mass from an elevation z > 0 (in a vacuum) will reach a speed
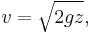 when arriving at elevation z=0. Or when we rearrange it as a head:
when arriving at elevation z=0. Or when we rearrange it as a head: 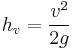
The term v2 / (2 g) is called the velocity head, expressed as a length measurement. It represents the internal energy of the fluid due to its motion.
The hydrostatic pressure p is defined as
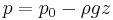 , with p0 some reference pressure, or when we rearrange it as a head:
, with p0 some reference pressure, or when we rearrange it as a head: 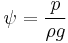
The term p / (ρg) is also called the pressure head, expressed as a length measurement. It represents the internal energy of the fluid due to the pressure exerted on the container.
When we combine the head due to the flow speed and the head due to static pressure with the elevation above a reference plane, we obtain a simple relationship useful for incompressible fluids using the velocity head, elevation head, and pressure head.
 (Eqn. 2b)
(Eqn. 2b)
If we were to multiply Eqn. 1 by the density of the fluid, we would get an equation with three pressure terms:
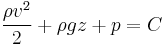 (Eqn. 3)
(Eqn. 3)
We note that the pressure of the system is constant in this form of the Bernoulli Equation. If the static pressure of the system (the far right term) increases, and if the pressure due to elevation (the middle term) is constant, then we know that the dynamic pressure (the left term) must have decreased. In other words, if the speed of a fluid decreases and it is not due to an elevation difference, we know it must be due to an increase in the static pressure that is resisting the flow.
All three equations are merely simplified versions of an energy balance on a system.
-
Bernoulli equation for compressible fluids The derivation for compressible fluids is similar. Again, the derivation depends upon (1) conservation of mass, and (2) conservation of energy. Conservation of mass implies that in the above figure, in the interval of time Δt, the amount of mass passing through the boundary defined by the area A1 is equal to the amount of mass passing outwards through the boundary defined by the area A2: 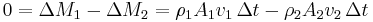 .
.
Conservation of energy is applied in a similar manner: It is assumed that the change in energy of the volume of the streamtube bounded by A1 and A2 is due entirely to energy entering or leaving through one or the other of these two boundaries. Clearly, in a more complicated situation such as a fluid flow coupled with radiation, such conditions are not met. Nevertheless, assuming this to be the case and assuming the flow is steady so that the net change in the energy is zero,
where ΔE1 and ΔE2 are the energy entering through A1 and leaving through A2, respectively.
The energy entering through A1 is the sum of the kinetic energy entering, the energy entering in the form of potential gravitational energy of the fluid, the fluid thermodynamic energy entering, and the energy entering in the form of mechanical p dV work:
where Ψ = gz is a force potential due to the Earth's gravity, g is acceleration due to gravity, and z is elevation above a reference plane.
A similar expression for
 may easily be constructed. So now setting
may easily be constructed. So now setting 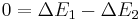 :
:which can be rewritten as:
Now, using the previously-obtained result from conservation of mass, this may be simplified to obtain
which is the Bernoulli equation for compressible flow.
Real world application
In modern everyday life there are many observations that can be successfully explained by application of Bernoulli's principle.
- Bernoulli's Principle can be used to calculate the lift force on an airfoil if you know the behavior of the fluid flow in the vicinity of the foil. For example, if the air flowing past the top surface of an aircraft wing is moving faster than the air flowing past the bottom surface then Bernoulli's principle implies that the pressure on the surfaces of the wing will be lower above than below. This pressure difference results in an upwards lift force.[nb 1][19] Whenever the distribution of speed past the top and bottom surfaces of a wing is known, the lift forces can be calculated (to a good approximation) using Bernoulli's equations[20]—established by Bernoulli over a century before the first man-made wings were used for the purpose of flight. Bernoulli's principle does not explain why the air flows faster past the top of the wing and slower past the underside. To understand why, it is helpful to understand circulation, the Kutta condition, and the Kutta-Joukowski theorem.
- The carburetor used in many reciprocating engines contains a venturi to create a region of low pressure to draw fuel into the carburetor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli's principle; in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.
- The Pitot tube and static port on an aircraft are used to determine the airspeed of the aircraft. These two devices are connected to the airspeed indicator which determines the dynamic pressure of the airflow past the aircraft. Dynamic pressure is the difference between stagnation pressure and static pressure. Bernoulli's principle is used to calibrate the airspeed indicator so that it displays the indicated airspeed appropriate to the dynamic pressure.[21]
- The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate, which can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, the continuity equation shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid flow speed. Subsequently Bernoulli's principle then shows that there must be a decrease in the pressure in the reduced diameter region. This phenomenon is known as the Venturi effect.
- The maximum possible drain rate for a tank with a hole or tap at the base can be calculated directly from Bernoulli's equation, and is found to be proportional to the square root of the height of the fluid in the tank. This is Torricelli's law, showing that Torricelli's law is compatible with Bernoulli's principle. Viscosity lowers this drain rate. This is reflected in the discharge coefficient which is a function of the Reynold's number and the shape of the orifice.[22]
- In open-channel hydraulics, a detailed analysis of the Bernoulli theorem and its extension were recently developed[23]. It was proved that the depth-averaged specific energy reaches a minimum in converging accelerating free-surface flow over weirs and flumes (also [24][25]). Further, in general, a channel control with minimum specific energy in curvilinear flow is not isolated from water waves, as customary state in open-channel hydraulics.
- The principle also makes it possible for sail-powered craft to travel faster than the wind that propels them (if friction can be sufficiently reduced). If the wind passing in front of the sail is fast enough to experience a significant reduction in pressure, the sail is pulled forward, in addition to being pushed from behind. Although boats in water must contend with the friction of the water along the hull, ice sailing and land sailing vehicles can travel faster than the wind.[26][27]
Misunderstandings about the generation of lift
Many explanations for the generation of lift (on airfoils, propeller blades, etc.) can be found; but some of these explanations can be misleading, and some are false. This has been a source of heated discussion over the years. In particular, there has been debate about whether lift is best explained by Bernoulli's principle or Newton's laws of motion. Modern writings agree that Bernoulli's principle and Newton's laws are both relevant and correct [28][29][30].
Several of these explanations use the Bernoulli principle to connect the flow kinematics to the flow-induced pressures. In cases of incorrect (or partially correct) explanations of lift, also relying at some stage on the Bernoulli principle, the errors generally occur in the assumptions on the flow kinematics, and how these are produced. It is not the Bernoulli principle itself that is questioned because this principle is well established.[31][32][33][34]
See also
- Terminology in fluid dynamics
- Navier-Stokes equations – for the flow of a viscous fluid
- Euler equations – for the flow of an inviscid fluid
- Hydraulics – applied fluid mechanics for liquids
- Venturi effect
References
- ↑ Clancy, L.J., Aerodynamics, Chapter 3.
- ↑ Batchelor, G.K. (1967), Section 3.5, pp. 156-64.
- ↑ "Hydrodynamica". Britannica Online Encyclopedia. http://www.britannica.com/EBchecked/topic/658890/Hydrodynamica#tab=active~checked%2Citems~checked&title=Hydrodynamica%20--%20Britannica%20Online%20Encyclopedia. Retrieved 2008-10-30.
- ↑ Streeter, V.L., Fluid Mechanics, Example 3.5, McGraw–Hill Inc. (1966), New York.
- ↑ 5.0 5.1 Batchelor, G.K. (1967), §5.1, p. 265.
- ↑ Mulley, Raymond (2004). Flow of Industrial Fluids: Theory and Equations. CRC Press. ISBN 0849327679., 410 pages. See pp. 43-44.
- ↑ Chanson, Hubert (2004). Hydraulics of Open Channel Flow: An Introduction. Butterworth-Heinemann. ISBN 0750659785., 650 pages. See p. 22.
- ↑ Oertel, Herbert; Prandtl, Ludwig; Böhle, M.; Mayes, Katherine (2004). Prandtl's Essentials of Fluid Mechanics. Springer. pp. 70–71. ISBN 0387404376.
- ↑ "Bernoulli's Equation". NASA Glenn Research Center. http://www.grc.nasa.gov/WWW/K-12/airplane/bern.htm. Retrieved 2009-03-04.
- ↑ 10.0 10.1 Clancy, L.J., Aerodynamics, Section 3.5.
- ↑ Clancy, L.J. Aerodynamics, Equation 3.12
- ↑ 12.0 12.1 Batchelor, G.K. (1967), p. 383
- ↑ Clarke C. and Carswell B., Astrophysical Fluid Dynamics
- ↑ Clancy, L.J., Aerodynamics, Section 3.11
- ↑ Van Wylen, G.J., and Sonntag, R.E., (1965), Fundamentals of Classical Thermodynamics, Section 5.9, John Wiley and Sons Inc., New York
- ↑ 16.0 16.1 16.2 Feynman, R.P.; Leighton, R.B.; Sands, M. (1963). The Feynman Lectures on Physics. ISBN 0-201-02116-1., Vol. 2, §40-3, p. 40-6 -- 40-9.
- ↑ Tipler, Paul (1991). Physics for Scientists and Engineers: Mechanics (3rd extended ed.). W. H. Freeman. ISBN 0-87901-432-6., p. 138.
- ↑ Feynman, R.P.; Leighton, R.B.; Sands, M. (1963). The Feynman Lectures on Physics. ISBN 0-201-02116-1., Vol. 1, §14-3, p. 14-4.
- ↑ Resnick, R. and Halliday, D. (1960), Physics, Section 18-5, John Wiley & Sons, Inc., New York ("[streamlines] are closer together above the wing than they are below so that Bernoulli's principle predicts the observed upward dynamic lift.")
- ↑ Eastlake, Charles N. Eastlake. "An Aerodynamicist’s View of Lift, Bernoulli, and Newton". THE PHYSICS TEACHER Vol. 40, March 2002. http://www.df.uba.ar/users/sgil/physics_paper_doc/papers_phys/fluids/Bernoulli_Newton_lift.pdf. "The resultant force is determined by integrating the surface-pressure distribution over the surface area of the airfoil."
- ↑ Clancy, L.J., Aerodynamics, Section 3.8
- ↑ Mechanical Engineering Reference Manual Ninth Edition
- ↑ Castro-Orgaz, O. & Chanson, H. (2009). Bernoulli Theorem, Minimum Specific Energy and Water Wave Celerity in Open Channel Flow. Journal of Irrigation and Drainage Engineering, ASCE, Vol. 135, No. 6, pp. 773-778 (DOI: http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000084) (ISSN 0733-9437).
- ↑ Chanson, H. (2009). Transcritical Flow due to Channel Contraction. Journal of Hydraulic Engineering, ASCE, Vol. 135, No. 12, pp. 1113-1114 (ISSN 0733-9429).
- ↑ Chanson, H. (2006). Minimum Specific Energy and Critical Flow Conditions in Open Channels. Journal of Irrigation and Drainage Engineering, ASCE, Vol. 132, No. 5, pp. 498-502 (DOI: 10.1061/(ASCE)0733-9437(2006)132:5(498)) (ISSN 0733-9437).
- ↑ Ice Sailing Manual, p. 2
- ↑ Wind Sports – Ice sailing hand held sails
- ↑ Chanson, H. (2009). Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages. ISBN 978-0-415-49271-3.
- ↑ "Newton vs Bernoulli". http://www.grc.nasa.gov/WWW/K-12/airplane/bernnew.html.
- ↑ Ison, David. Bernoulli Or Newton: Who's Right About Lift? Retrieved on 2009-11-26
- ↑ Phillips, O.M. (1977). The dynamics of the upper ocean (2nd ed.). Cambridge University Press. ISBN 0 521 29801 6. Section 2.4.
- ↑ Batchelor, G.K. (1967). Sections 3.5 and 5.1
- ↑ Lamb, H. (1994) §17-§29
- ↑ Weltner, Klaus; Ingelman-Sundberg, Martin. "Physics of Flight - reviewed". http://user.uni-frankfurt.de/~weltner/Flight/PHYSIC4.htm. "The conventional explanation of aerodynamical lift based on Bernoulli’s law and velocity differences mixes up cause and effect. The faster flow at the upper side of the wing is the consequence of low pressure and not its cause."
Notes
- ↑ Clancy, L.J., Aerodynamics, Section 5.5 ("When a stream of air flows past an airfoil, there are local changes in flow speed round the airfoil, and consequently changes in static pressure, in accordance with Bernoulli's Theorem. The distribution of pressure determines the lift, pitching moment and form drag of the airfoil, and the position of its centre of pressure.")
Further reading
- Batchelor, G.K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 0521663962.
- Clancy, L.J. (1975). Aerodynamics. Pitman Publishing, London. ISBN 0273011200.
- Lamb, H. (1993). Hydrodynamics (6th ed.). Cambridge University Press. ISBN 9780521458689. Originally published in 1879; the 6th extended edition appeared first in 1932.
- Chanson, H. (2009). Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group. ISBN 978-0-415-49271-3.
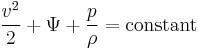
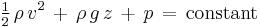
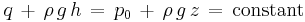
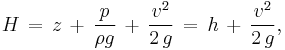
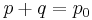
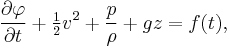

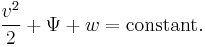
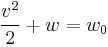

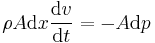
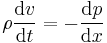
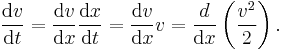


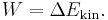
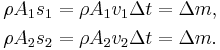
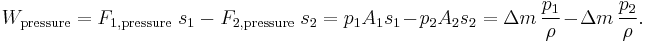
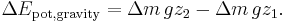
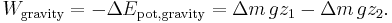
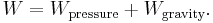
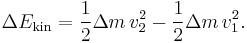
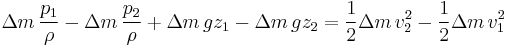
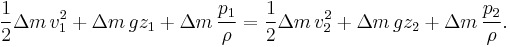
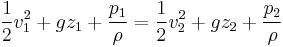
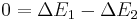
![\Delta E_1 = \left[\frac{1}{2} \rho_1 v_1^2 + \Psi_1 \rho_1 + \epsilon_1 \rho_1 + p_1 \right] A_1 v_1 \, \Delta t](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d7dc9db6ffd7dd534e3063a75c3ddec0.png)
![0 = \left[\frac{1}{2} \rho_1 v_1^2+ \Psi_1 \rho_1 + \epsilon_1 \rho_1 + p_1 \right] A_1 v_1 \, \Delta t - \left[ \frac{1}{2} \rho_2 v_2^2 + \Psi_2 \rho_2 + \epsilon_2 \rho_2 + p_2 \right] A_2 v_2 \, \Delta t](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/307ff04dd5267d3c26bab53b54ed3637.png)
![0 = \left[ \frac{1}{2} v_1^2 + \Psi_1 + \epsilon_1 + \frac{p_1}{\rho_1} \right] \rho_1 A_1 v_1 \, \Delta t - \left[ \frac{1}{2} v_2^2 + \Psi_2 + \epsilon_2 + \frac{p_2}{\rho_2} \right] \rho_2 A_2 v_2 \, \Delta t](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ffe9fe16a1a66969b5615666c7d60aaf.png)